Knapsack Problem은 담을 수 있는 물건의 크기가 정해져있을 때 가치의 합이 가장 크도록 물건을 담게 하는 방법이다.
알고리즘은 다음과 같다.
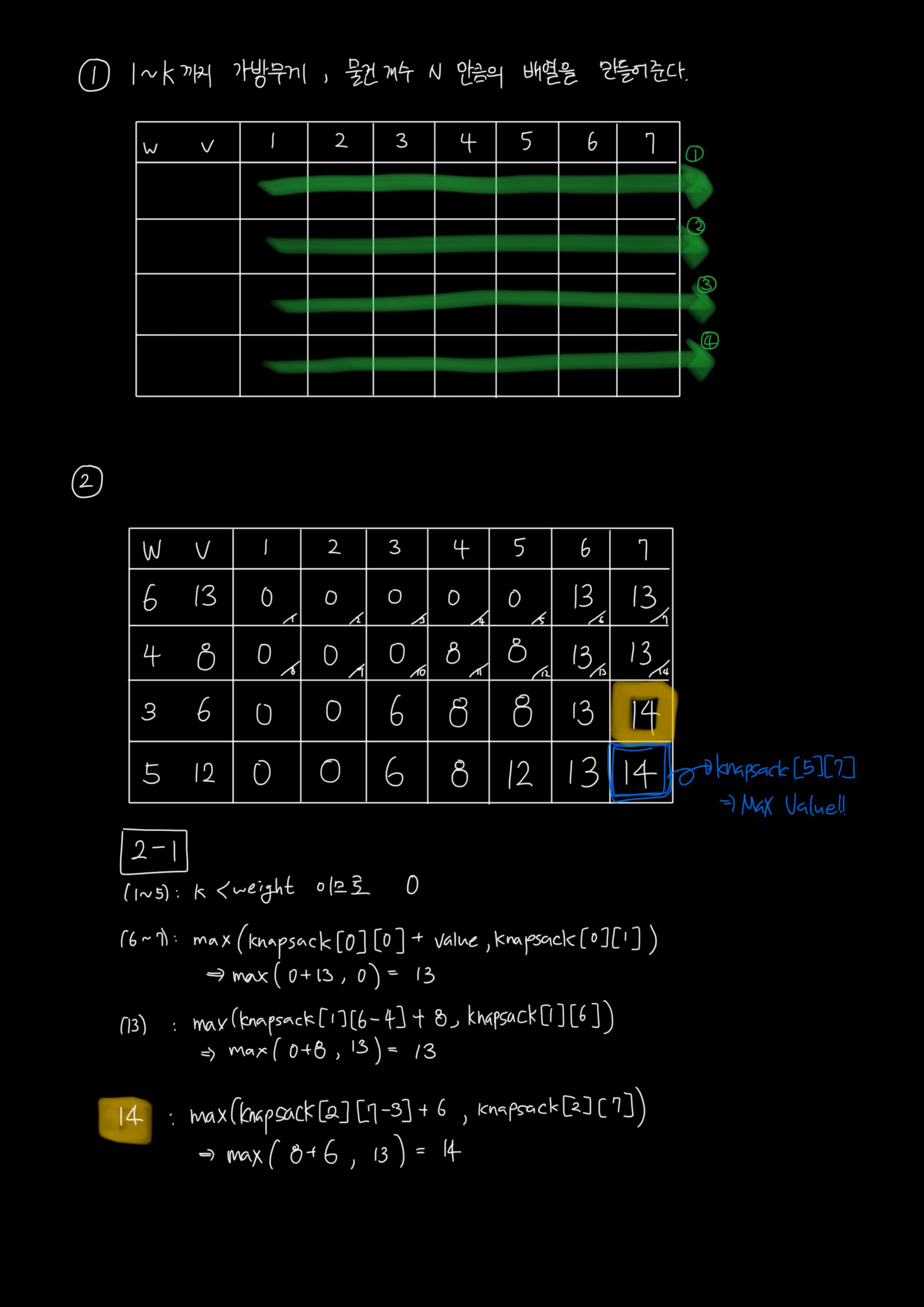
1) x축엔 가방 1~K 까지의 무게, y축은 물건 N개 개수 만큼의 배열을 만들어준다.
2) 행을 차례대로 돌며 다음과 같은 알고리즘을 수행해준다.
3-0) 현재 물건이 현재 돌고있는 무게보다 작다면 바로 [이전 물건][같은 무게] (knapsack[i-1][j]를 입력해준다.
3-1) 현재 물건을 넣어준다. 물건을 넣은 뒤의 남은 무게를 채울 수 있는 최댓값(knapsack[i-1][j-weight]을 위의 행에서 가져와 더해준다.
3-2) 현재 물건을 넣어주는 것보다. 다른 물건들로 채우는 값(knapsack[i-1][j])을 가져온다.
4) 3-1과 3-2 중 더 큰 값을 knapsack[i][j]에 저장해준다. 이 값은 현재까지의 물건들로 구성할 수 있는 가장 가치 높은 구성이다.
5) knapsack[N][K]는 곧, K무게일 때의 최댓값을 가리킨다.
참고: https://claude-u.tistory.com/208
백준 12865번
문제:
첫 줄에 물품의 수 N(1 ≤ N ≤ 100)과 준서가 버틸 수 있는 무게 K(1 ≤ K ≤ 100,000)가 주어진다. 두 번째 줄부터 N개의 줄에 거쳐 각 물건의 무게 W(1 ≤ W ≤ 100,000)와 해당 물건의 가치 V(0 ≤ V ≤ 1,000)가 주어진다.
입력으로 주어지는 모든 수는 정수이다.

문제를 풀기 위해 다음과 같은 배열을 만들어볼 수 있다.
'알고리즘' 카테고리의 다른 글
| 그리디 알고리즘_JAVA (0) | 2023.09.12 |
|---|---|
| [프로그래머스] 성격 유형 검사하기 by Python (0) | 2022.09.02 |
| [그래프] 벨만-포드 알고리즘 (0) | 2022.01.12 |
| [우선순위 큐- heapq] 백준 1655 (0) | 2022.01.04 |
| [22935번][PYTHON] 백준 22935번 - 이진 딸기 (0) | 2021.08.18 |